|
逆数除算 |
|
高次収束 |
| 最終更新日:2006/12/30 図表改訂 |
●概要
紹介したのは、2次収束と呼ばれるが、3次から5次などの収束もある。次数倍づつ精度があがるので、良さそうに見えるが、実際には、収束回数が減った分、演算数が増加するので、ほぼチャラとなってしまう。つまり、回数 * 演算数 = ほぼ同じ になる。
●漸化式
- 3次収束
d = 1 - A * Xn
Xn+1 = Xn * (1 + d + d2)
- 4次収束
d = 1 - A * Xn
Xn+1 = Xn * (1 + d) * (1 + d2)
- 5次収束
d = 1 - A * Xn
Xn+1 = Xn * (1 + (1 + d2) * (d + d2))
それぞれの d の指数部を収束条件に使用する。
●方式の得失
演算時間が短くなるものを選ぶことになる。高次で収束回数が減少しても、ループ当りの演算時間が増加するので、一概に良いとは言えない。それぞれの演算数は、以下の表のようになる。
| 演算 | 2次収束 | 3次収束 | 4次収束 | 5次収束 |
| 乗算 | 2 | 3 | 4 | 4 |
| 加減算 | 2 | 3 | 3 | 4 |
精度が上がれば乗算時間が支配的となるので、2次収束が演算数上では有利となる。4次と5次では乗算数が同じであるので、5次が有利と予測できる。下図はシミュレータで次数 による演算時間を予測したものである。初期値は15桁。薄緑色の部分がその桁での最小時間。
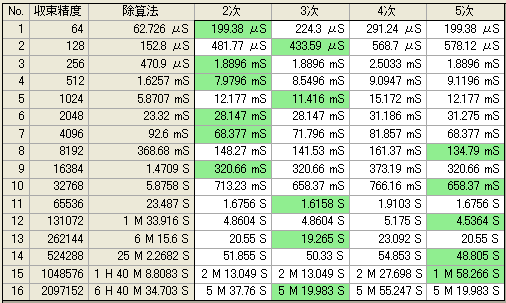
ほぼ同じ傾向で、劇的な差はない。 精度が高い部分では5次が有利と出た。予想通り、4次が最も不利となっている。但し、求める精度と収束回数は非線形(量子化状態)なので、一般に関係は複雑になる。
総合的に判断して、2次収束で十分となった。