|
FFT乗算 |
|
FFT乗算の原理 |
| 最終更新日:2007/04/26 見直し |
●概要
導入にあたり、フーリエ変換やFFTはあるものとして、FFT乗算についての原理と乗算の方法を調べた。
●原理
フーリエ変換は、数学的には 直交変換(積分変換)の一つで、信号(一次元、二次元、画像、物体など、データであれば結局何でも良い)を全く別の切り口で表現するものである。フーリエ変換では、周期関数の集合として表現する。離散系では有限の集合となる。実空間では距離などであったものが、フーリエ空間では、周波数と 解釈すればよい。ここでは、フーリエ変換には言及しないので、他書に依られたい。
○畳み込み
重要な数学演算に、畳み込み(コンボリューション)がある。これは、ある関数 f に、別の関数 g を重畳させる演算である。通常、f*g と表す。連続空間では畳み込み積分となる。これは、一言で言えば、あるデータ群に対して、一定の変形を連続的に施すことになり、例えば、フィルタを掛けるイメージとなる。畳み込みは離散系でもあり、この場合は、積分ではなく、総和となる。離散系の畳み込みのk番目の要素は、
(f*g)(k) = ∑f(n)*g(k-n)
と表される。但し、離散系では区間が有限であるため、周期関数と見なされ、循環畳み込みとなる。つまり、f が区間を周期として繰り返し現われるとしている。ちなみに、連続系では、-∞から+∞の線形畳み込みとなる。
○多項式の掛算
さて、f、g を多項式の係数列とすれば、簡単のため、3要素とすると、その掛算は、
| f0 | f1 | f2 | ||
| g0 | g1 | g2 | ||
| f0*g2 | f1*g2 | f2*g2 | ||
| f0*g1 | f1*g1 | f2*g1 | ||
| f0*g0 | f1*g0 | f2*g0 | ||
| f0*g0 | f0*g1+f1*g0 | f0*g2+f1*g1+f2*g0 | f1*g2+f2*g1 | f2*g2 |
となる。最下段が積の結果である。これは、実は、離散系の畳み込みに他ならない。しかも、筆算で行う数値の掛算とも同じである。但し、筆算の掛算では、随時桁上げ処理を行うことが異なっている。数値も多項式であるから、数値の掛算も、離散系の畳み込みと同じと言える。
○畳み込み定理
フーリエ変換の重要定理に、畳み込み定理がある。それは、
F(f*g) = F(f)・F(g)
で、実空間の畳み込みのフーリエ変換は、元の関数のそれぞれのフーリエ変換の単純な積(要素同士)になる。下図のようになる。乗算回数が、N2 から N になる。これは、例えば、フィルタ(周波数フィルタ)では、フーリエ空間では、要素が既にそれぞれの周波数成分なので、それぞれの成分を個々に補正(フィルタリング)すれば良い・・・と言うイメージを浮かべてもらえば分かり良い。
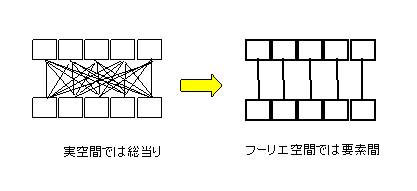
もう、お分かりと思うが、数値を多項式と見立てて(本来は多項式なのだが)、多項式の乗算、即ち、離散系の畳み込みをフーリエ空間で行い、それを実空間に戻して、数値の乗算をしたことにするのである。
今、4096個(まあ、桁と思って良い)の一次元データに4096個データの一次元フィルタを掛けるとすれば、実空間では、4096*4096 約1678万回の乗算が必要となるが、DFTでは、畳み込みだけでは、0.4万回で済む。前後に3回のDFTが必要となるが、この分は、FFTで行えば8万回程度なので、約8.4万回で済むことになる。約200倍のスピードとなる。
FFTにより、畳み込みがDFTで現実的に行えるようになり、今日の隆盛を見ているのである。
●方法
○数値の扱い
DFTではサンプリングデータ列 a(i) が入力となる。今、乗算したい数値N を、多項式とすれば、
N = ∑(ai * Bi)
と表せる。つまり、数値N は基底数B のB進数表現に他ならない。MegaLong では、B = 100,000,000 となっている。この多項式の、ai を、サンプリングデータ列 a(i) と思えば良い。
○FFT乗算の方法
- 被乗数、乗数をデータ列、a(i)、b(i) とする。配列の要素数を偶数にし、かつ乗算結果は、二つの配列サイズの合計になるので、a、b とも、2倍にし、後半に0を埋める。つまり、3者同じサイズにする。これは、循環畳み込みの弊害(折り返し誤差など)を避け、線形畳み込みにしていることになる。
- a(i)、b(i) のフーリエ変換、A()、B() を求める。複素数の乗算が必要。
- A()、B() の同じ要素同士の乗算(つまり、コンボリューションする)を行い、これをC() とする。
- C() を逆フーリエ変換する。これをc() とする
- c() は、基底数を越える部分が出てくるので、桁上げを行う、あるいは、桁合せを行う。筆算でもやっている筈。これが、乗算結果となる。最後の要素は常に 0 となる。c() では、かなりの項目数の総和となり(中央の項が最も多くなる)、下手をすればオーバーフローすることが考えられる。整数演算では、基数の選択が重要となる。.NETでは、Doubleの有効整数桁を超えない範囲に設定する必要がある。