|
逆数除算 |
|
初期値 |
| 最終更新日:2007/04/26 見直し |
●概要
初期値は何でも良いと言う訳ではなく、その後収束を決定付ける大切な要素である。多倍長の場合は、一般には、CPUネイティブ除算で、逆数を求め初期値にする。.NET の場合は、Double による初期値なので、15桁程度の精度となる。一般に、初期値の精度の次数倍づつ精度が上がるとされている。
●収束方程式
2次収束での収束を式で表すと、
DF = 2n・DS
DF :目標精度桁数
n :収束回数
DS :初期値精度桁数
となる。上式を変形し、DF = 2F 、DS = 2S とし、2 の対数を取れば、
n = -S + F
とむちゃくちゃ簡単な式が得られる。この式で、S = F とすれば、回数は 0 となる。漸化する必要なしとなるので、なんとなく正しいような気がする。
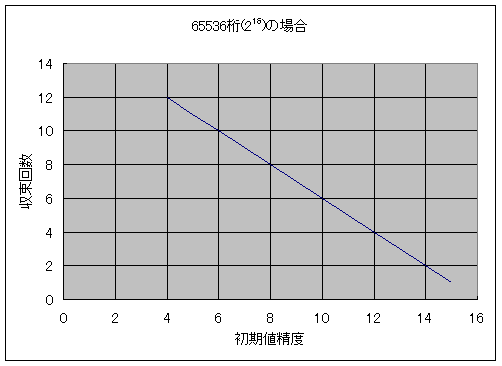
目標精度が65536桁の場合
●高い精度で演算する
例えば、初期値を 1024桁、つまり 210 からスタートすれば、上図から、収束回数は6回となる。この初期値は、通常の精度16桁、つまり 24 から求めるとすれば、収束回数は同じく6回となる。結局合計の回数は一定となる。しかし、1024桁の精度では、1024桁の精度で演算すれば良いのだから、演算時間は減るはずである。
ニュートン漸化式の単位演算時間を f(X) (X は演算精度) とすれば、上のことは以下の式で表現できる。
通常の初期値による演算時間 Tu = n・f(Xm)
中間精度による演算時間 Tc = n1・f(Xc) + n2・f(Xm)
となる。一般に、FFT乗算なので、f(X) は一次関数以上の次数となる。ところで、
n1 + n2 = n
なので、n2 = n - n1、だから、
Tc = n1・f(Xc) + n2・f(Xm)
= n1・f(Xc) + (n - n1)・f(Xm)
= n1・(f(Xc) - f(Xm)) + n・f(Xm)
となる。ところが、f(Xc) - f(Xm) < 0 である(少なくとも単調増加関数で Xc < Xmなので)ので、結局、
Tc < Tu
となる。つまり、中間の初期値で演算した方が速くなることになる。FFT乗算では、一般には、f(X) ∝ g(X)log(g(X)) と、一次よりは次数が高いので、より期待は持てる。
下図は、2次のニュートン漸化式をシミュレーションした結果である。

前半

後半
15の列が通常初期値の場合の演算時間で、64、128 と中間初期値を変化した場合の演算時間の表である。緑色が、その目標精度で最も速かった中間初期値となる。
●多段初期値
上記を、中間の初期値を求める場合にも適用(相似)すれば、元より速くなると言える。これを一般化すれば、演算精度を徐々に上げながら、複数の初期値を順々に求めていけば、更に速くなると思われる。
T = ∑ni・f(Xi) < Tu
但し、n = ∑ni
である。但し、演算精度を徐々に上げながら が本法のミソである。
下図は、多段初期値方式を2次のニュートンでシミュレーションした結果である。 参考値として、15桁単一初期値、1/4中間初期値(収束精度の1/4桁の中間初期値)もシミュレーションしているので、その改善効果かが分かる。
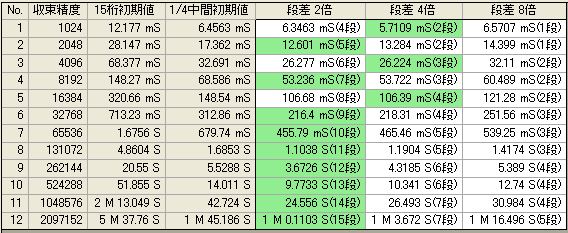
-
段差2倍とは、次の初期値の桁数が、その回の倍となることで、64→128→256→512→1024 などとなる。
-
段差4倍とは、64→256→1024 など
-
段差8倍とは、64→512→4096 など
●実測値
準備中