[ ホーム ] [ 概要 ] [ プログラミング仕様 ] [ 演算速度 ] [ 技術解説(システム編) ] [ 技術解説(四則演算編) ] [ 技術解説(FFT編) ] [ 技術解説(数学関数編) ]

上へ
多倍長語 MegaLong
基数変換
数値変換
定数システム
演算時間予測システム

●概要

　構造体 MegaLongは、MegaPrecision で使用される数値であるが、世の中との互換性はない。 10進の浮動小数点形式となっている。

　10進にしたのは、通常科学演算では10進であること、2進の小数で10進を表現する場合、無限循環小数になることがあること(有名なのは、0.1 )、人間に分かる10進表示では、2進数の場合、基数変換が重くなる(厄介で時間が掛かる処理となる)・・・などの理由である。

●構造

○構造体仕様

  Public Structure MegaLong
     Friend Mant() As Integer
     Friend Sign As MegaSign
     Friend Exp As Integer
     Friend Length As Integer

    (New、プロパティ、メソッドあり)

　End Structure

○符号

　MegaLong は以下のEnum にて符号を表す。

  Public Enum MegaSign
     Negative = -1
     Zero = 0
     Positive = 1
     Overflow = 2
     NaN = 3
  End Enum

●形式

　符号、仮数、指数からなる。仮数部は、10⁸(1億)を基数としたBCDで、 0 超過、1 未満を表す。

　± 0.9999・・・・・・9999 ±指数 (10^±指数)

数式で表現すれば、

  Sign・Σ(a_i・10^-8・(i+1))・10^Exp(i = 0 to n - 1、Sign = -1 or 1)

  但し、10⁸ ＞ a₀ ≧ 10⁷、10⁸ ＞ a_i ≧ 0 (i>0)　が正規化状態

が、一般形式となる。

○符号(Sign)

• 仮数部の正負を表す。従って、仮数部は常に正。
• 値 0 の場合も、符号にて、Zero 表示する。
• OverflowやNaN(非数値)も表す。

○仮数部(Mant())

　可変長のInteger配列で表されており、仮数部は可変長となるので、精度(桁数)に応じて最適化される。一つの配列にて、0〜99999999(1億 - 1、10進8桁)を表す、1億進数となっている(当然、実際の値は2進数となっている。)。但し、小数を表すので、保有される値は左よりになっている。小数点は、Mant(0) の直ぐ左にあるとなっている。

　仮数部の先頭(Mant(0)) は、必ず、10000000 (10⁷) 以上となるように正規化されている。数値で言えば、小数点1位が必ず、1以上と言うこと。

　例えば、0.123456780987 は、配列数が2となり、下図のように表される。

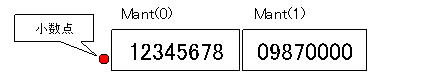
○指数(Exp)

　範囲は Integer の範囲なので、およそ、10 の±21億乗 となる。単純にLong にすればもっと範囲は広がる。

○桁数(Length)

　仮数部で、先頭から最後の0でない10進1桁までの桁数を示す。例えば、0.12345678000000001 では、17 となる。仮数部を検査すれば分る値であるが、検査に時間が掛かるので、正規化のときに設定される。

●演算

　この方式で実際に演算できることを以下に解説する。

○加算

・実数値演算

 5 + 8 = 13

・仮数部演算

　数値の 5 は、内部では、0.5E+1 となるので、50000000 指数1 と表現されている。つまり、

　5 = 50000000*10^-8*10¹

である。以降、これを例えば、5000000(1) と略記する。

 50000000(1) + 80000000(1) = 1|30000000   ()は指数部、| は、8桁区切り

この例では、同じ指数なので桁合せは不要。

・正規化

1|30000000(Long値) を、基数1億で整数除算すると、1(キャリー) となり、同じく Mod すれば、30000000 が得られる。これにて　キャリー 1 と、 30000000 なる仮数部になるが、規定により、この仮数部は、1桁シフトダウンされる(つまり、キャリーを頭に持ってくる)。結局、13000000 が規格化で得られる。シフトダウンすることで、指数部は +1 されて補正され、2 になる。つまり、13000000(2)で、これは、13を表す。

○乗算

・実数値演算

0.500000005 * 1111111111 = 555555561.055555555

・仮数部演算

50000000 50000000(0) * 11111111 11000000(10)

の乗算となるが、配列の要素間の部分積の総和となる。分かりやすくするために、それぞれの要素に記号 a、b、c、d を付けてある。

                                                              a 50000000 b 50000000
                                                              c 11111111 d 11000000
-----------------------------------------------------------
                                a*d 550000000000000　b*d 550000000000000
a*c 555555550000000  b*c 555555550000000

x*y は部分積でLong値とする。乗算では、この部分積を基数で規格化しながら加算し、Integer配列の仮数に変換する作業を行う。

b*d 5500000|00000000 (| は、8桁区切り) は、5500000 がキャリーで、結果は、00000000 となる。最下位決定。

a*d 550000000000000 + b*c 555555550000000 + 5500000 = 11055555|55500000は、キャリーが、11055555 結果が、55500000 となる。

a*c 555555550000000 + 11055555 = 5555555|61055555は、キャリーが、5555555 結果が、61055555 となる。結局、

05555555 61055555 55500000 00000000

なる非正規化仮数部が得られる。

・規格化

頭の配列要素を規定の形式にするため、仮数部を左に1桁シフト(頭出し)する(全体を10倍する)。このシフトにて、指数部を -1 補正する。また、末尾の0は除外する。乗算なので指数部は加算となり、0 + 10 = 10 であるが、-1 補正し、9 となる。

55555556 10555555 55000000(9) これは、555555561.055555555 を表す。

○除算

簡単のため、双方が基数(Base = 1億)未満の場合。

・実数値演算

 125 / 5 = 25

・仮数部演算

 12500000(3) / 50000000(1)

この例ではネイティブな除算命令で行う。

1.  12500000 / 50000000  = 00000000 ・・・ 12500000   (・・・は余りを示す)
2. 以下は、仮数部における小数部演算となる
   (12500000 * Base + 00000000) / 50000000 = 25000000 ・・・ 00000000
3. 余りが 0 なので終了。

取りあえずの商は、

00000000.25000000

となる。

・正規化

　頭の0要素を除去し、頭出し(この例では不要)し、指数部は除算なので、3 -1 = 2 となる。

  25000000(2) これは 25 を表す。