[ ホーム ] [ 概要 ] [ プログラミング仕様 ] [ 演算速度 ] [ 技術解説(システム編) ] [ 技術解説(四則演算編) ] [ 技術解説(FFT編) ] [ 技術解説(数学関数編) ]

上へ
多倍長語 MegaLong
基数変換
数値変換
定数システム
演算時間予測システム

●概要

　数学の関数を級数やニュートン法などにより算出させる場合、その演算速度を知るためには、実測するのが一番良いが、関数によっては精度があがると、数十時間、数日間に及ぶものがある。これでは計測は困難である。

　そう言うことで、今まで筆者は、級数などに含まれる基本演算(主として四則算)の組合せを抽出し、エクセルなどを利用してマニュアルで演算速度を算出してきた。これは、当らずとも遠からずで、目安になった。有用であるが面倒くさい方法である。

　今回、これをシステム化し、パラメータなどを与えると自動的に算出する仕組みを構築したので紹介する。

●構成

　予測システムは大きく、以下の二つがある。

• 収束予測
  
  級数、ニュートンなどの収束を予測する。
  　
• 時間予測
  
  MegaPrecision での基本演算時間予測を予測する。
  　

　下図の赤枠の部分である。

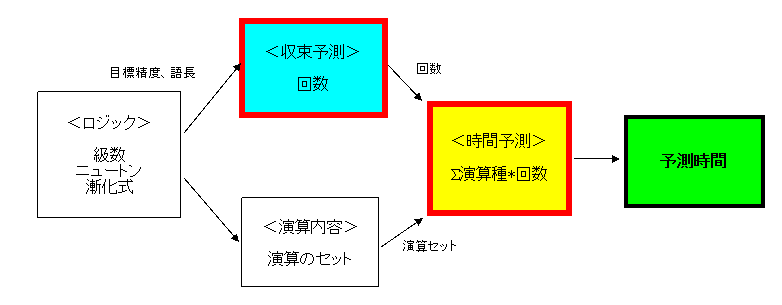
●予測方法

　フローは上図のようになる。時間を予測したい数学関数などがあるとすれば、以下のようにする。

1. その関数値を求めるロジックを決める。

2. 求めたい精度や変数の語長などによって、収束予測を行う。

3. 一方、ロジックが決まれば、その演算内容も決まり、単位当たりの演算内容もきまる。

4. 収束回数と演算セットを時間予測に与えれば、積和すれば全時間が予測される。

●収束予測

　級数やニュートン法では、時間を予測するには収束を予測しなければならない。

●収束予測関数

　MegaPrecision で用意されている予測(関数)の原理を解説する。

○階乗予測

　級数には、階乗が現われる。従って、k! のオーダや、10^P になる k! の k を見つける必要がある。

○級数予測

　級数には種々あるが、良く見ると数種の型に分類できる。それらの型につき、変数のオーダによる収束を予測する。

●時間予測

　実測値から演算時間表を生成し、それらを使い演算時間を予測する手法を解説する。　

○時間予測の仕組み

　下図のようになっている。中心となるのは、赤太枠の演算時間表(群)で、予め実測された値を元に生成される。おおむね、以下のような手順で時間が予測される。

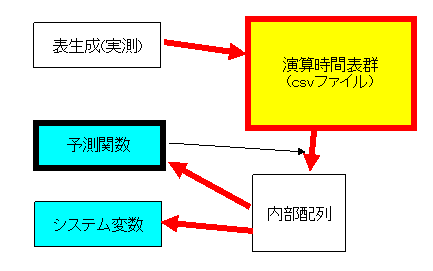
1. 演算時間を問う時間予測関数が実行されると、

2. 引数で指定された演算種によって必要な演算を特定し、必要なテーブルを決める。

3. そのテーブルが内部配列になければ、ファイルから読み出す。次回からは内部配列を使用する。

4. 指定された精度に従ってテーブルを一次補間して値(時間)を算出する。

5. 予測関数によっては、演算セットが指定されているので、必要な全ての時間を算出し、積和する。

○時間表の生成　

　実測値を元に幾つかの時間表が生成される。

○限界値自動決定

　限界値とは、乗除算に関連するシステム変数で、FFTLimit、ReciproLimit、MulSLimit のことであるが、これらの値は、固定ではなく、実装された環境で決まる変数となる。つまり、総合的な演算能力で変動する。最適値は、システム毎に実測すべき値となる。