|
VB.NET2005 TIPS / 理数系 |
|
S0003 陰関数のグラフ |
| 最終更新:2006/11/12 旧版統合 |
●解説
陰関数は f(X,Y)=0 と言う形の関数で、y=g(X) の形が存在する場合と存在しない(数学上表現できない)場合がある。これのグラフは、陽関数形がない(分からない)とすれば、かなり厄介なものとなる。世の中には、陰関数を y=g(X) の形にできるものは記号演算して求めそれをグラフ化する高度な数学ソフトがある。 また、媒介変数を導入して数式を変形しグラフを描く場合もあるが一般に媒介変数で表せる保証はない。ここのポリシーはあくまで、関数をブラックボックスとして扱い任意の陰関数を直接グラフとして描く方法を紹介する。 例によって、実現方法は我流なので、数学的な美しさはない。
●原理(筆者が適当に考えついたもの)
厄介と言ったが原理はしごく簡単で、与えられたX、Yの範囲で、全てのX、Yを代入し、関数値が 0 になるX、Yを見つける力技である。時間が掛かるだけで難しくはない。以下のような方法が考えられる。名称は筆者が適当に付けたもので世の中で使われている訳ではない。
陽関数や媒介変数ではないので、曲線は連続した線としては求められないく、点集合として求められるだけである。これを描画すると曲線に見えるだけである。
1.真っ向法 ×
真っ正直に f(X,Y)=0 になるXとYを求める(機械的に、X,Yをスキャンして、ひたすら =0 を探す)。しかしこれは見事に失敗する。f(X,Y)=0
となるX,Yは偶然見つけられる程度で、一般的には曲線として成立するほど見つからない。正直者が報われない典型例。
2.閾値法 △〜○
閾値zを導入し、0=<|f(X,Y)|=< z になるX,Yを見つける。これは成功するが、z
の適正値に一般解がないので、試行錯誤的になるし、求められた曲線は有限の幅を持ったもの(ソリッドな図形)となり、幅1ピクセルの曲線のグラフにはならない。しかし、この方法は、閾値を逆手に利用すれば、別な効果が得られる。
3.細線化法 ×
閾値法で得られたソリッド図形の中心線を細線化技法(Thinning)で求め、幅1ピクセルの曲線とする方法。しかし、閾値の大きさによるソリッドの太り具合で、必ずしも真の中心線が求まる訳でもないし、エイリアスも生じる。また、交差部分は大抵歪んでしまう。数学としてグラフを見たい時はやめた方が良い。実際に確かめた結論である。
4.ゼロクロス予測法 ◎
筆者がたどり着いた方法である。f(X,Y)=Z としたとき、Zが0に近づき、通過して離れていく場合、Yを固定して考えると、Xに対するZは、値0にならないものの、必ず0ラインを交差して行くはずである。つまり、Zの極性が反転する。この反転するXの隣り合う組の間に0になるXがあると予測できる。関数は二次元なので、X方向、Y方向で同じ極性反転ポイントを予測すれば良い。
ここでは、閾値法とゼロクロス法を紹介する。
有名な X3-3XY+Y3 デカルトの葉線のグラフを上記の二法で求めた例を示す。
|
|
|
| 閾値法 グレーモード、閾値=0.05 | ゼロクロス法 |
●閾値法
○解説
閾値は元の関数によって効果が変化するので、パラメータとする。この方法は、閾値による思わぬ幾何学模様 を得るのを目的とする。ここでは、閾値範囲を全て黒にするソリッドモードとその範囲をグレーレベルで変化させるグレーモードを紹介する。


Sin(3*X) + Cos(3*Y) 左:グレーモード、閾値=0.5、右:ソリッドモード
点の集合でかつ点同士の関係がないとすれば、扱うにはビットマップが良い。Point構造体で点を表すと、処理時間が膨大になりかつ、再描画にも時間が掛かり(これは耐えがたい)、実用できない。またここでは単純化のため、ビットマップのサイズと関数のX,Yの範囲を1:1に対応させる。また、X,Yの範囲幅は同じとする。つまり、関数領域は正方形で表示も同じ。
初期のグラフを求めるのに数秒から数十秒掛かるが、ビットマップのお陰で再描画は一瞬で終わる。
関数値の絶対値をF、閾値をDとすれば、
・F > D のとき、点の色を白とする。(情報としては捨てる)
・F = 0 のとき、点の色を黒レベルとする。(稀であるが一応)
・0 < F =< D のとき、 F / D * 255 値に応じたグレーレベル(グレーモード) または、黒レベル(ソリッド)
○実例
関数は文字列で任意に与えられるようにし、X,Yの初期値と範囲の幅、閾値を指定できる。
txtXsはX開始値の入力テキストボックス
txtYsはY開始値の入力テキストボックス
txtVWはX,Yの範囲幅入力テキストボックス
txtFは関数の入力テキストボックス
txtDは閾値の入力テキストボックス
chkGrはグレースケール変換のチェックボックス
Dim Act As Boolean = False
Dim bmp As Bitmap
Dim MySF As SmartFormula.SmartFormula
Dim WH As Integer = 300
'表示領域
Dim Xs, Ys, VW As Double
Private Sub btnS_Click(ByVal sender As System.Object, ByVal e As
System.EventArgs) Handles btnS.Click
Dim i, j As Integer
Dim F, dX, dY, D As Double
Dim GS As Color
If txtF.Text = "" Then Exit Sub
MySF = New SmartFormula.SmartFormula(txtF.Text)
If MySF.FormulaComplete <> 0 Then Exit Sub
Me.Cursor = Cursors.WaitCursor
Xs = txtXs.Text
Ys = txtYs.Text
VW = txtVW.Text
dX = VW / WH
dY = VW / WH
bmp = New Bitmap(WH + 1, WH + 1,
Imaging.PixelFormat.Format32bppArgb)
Dim g As Graphics = Graphics.FromImage(bmp)
g.Clear(Color.White)
g.Dispose()
D = txtD.Text
For i = 0 To WH
For j = 0 To WH
F = Abs(MySF.FunctionValue(Xs +
i * dX, Ys + j * dY))
If F <= D Then
'閾値より大きい場合は捨てる
If F = 0 Then
GS = Color.Yellow
Else
If chkGr.Checked Then
F = F / D * 255 '0でなければ、対応するグレーレベルに変換する
GS = Color.FromArgb(255, F, F, F)
Else
GS = Color.Black
'ベタ
End If
End If
bmp.SetPixel(i, WH - j, GS)
End If
Next
Act = True
Me.Invalidate()
'途中経過を表示
Application.DoEvents()
Next
End Sub
Private Sub frmImpF_Paint(ByVal sender As Object, ByVal e As
System.Windows.Forms.PaintEventArgs) Handles MyBase.Paint
If Act = False Then Exit Sub
Dim g As Graphics = e.Graphics
Dim Rec As New Rectangle((Me.ClientSize.Width - WH) / 2, 10, WH,
WH)
Dim X0, Y0 As Single
g.DrawImage(bmp, New PointF(Rec.Left,
Rec.Top))
'以下はスケール表示
Dim fmt As New StringFormat()
fmt.Alignment = StringAlignment.Center
fmt.LineAlignment = StringAlignment.Near
g.DrawString(Format(Xs, "0.##"), Me.Font, Brushes.Black, Rec.Left,
Rec.Bottom + 5, fmt)
g.DrawString(Format(Xs + VW, "0.##"), Me.Font, Brushes.Black,
Rec.Right, Rec.Bottom + 5, fmt)
If Xs < 0 And Xs + VW > 0 Then
X0 = Rec.Left + Rec.Width * (0 - Xs) / VW
g.DrawString("0", Me.Font, Brushes.Black, X0,
Rec.Bottom + 5, fmt)
End If
fmt.Alignment = StringAlignment.Far
fmt.LineAlignment = StringAlignment.Center
g.DrawString(Format(Ys + VW, "0.##"), Me.Font, Brushes.Black,
Rec.Left - 5, Rec.Top, fmt)
g.DrawString(Format(Ys, "0.##"), Me.Font, Brushes.Black, Rec.Left -
5, Rec.Bottom, fmt)
If Ys < 0 And Ys + VW > 0 Then
Y0 = Rec.Bottom - Rec.Height * (0 - Ys) / VW
g.DrawString("0", Me.Font, Brushes.Black,
Rec.Left - 5, Y0, fmt)
End If
End Sub
●ゼロクロス法
○解説
陰関数f(X,Y) は二次元関数であるが、関数値をZと置き、XY平面に垂直な軸とすれば曲面となる。この時、Z=0 の平面と交差する部分をXY平面上で見れば f(X,Y)=0 の曲線(グラフ)に他ならない。関数値つまりZを求めるX、Yの間隔は有限であり、無限小にはできないので、Z=0となるのは稀であるが、Z=0となる前後のXまたはYでは極値でない限り符号の反転が起こっている。 下図参照。
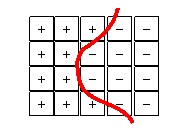
f(X,Y)=0 は、赤線と予測できる
関数は二次元なので、上記のようにX軸方向のみの処理では等方でなくなる(例えばX軸に平行な線は検出できない)ので、Y軸方向も同じ処理を施す。
最終的には表示が目的なので、ピクセル間隔以下で求める必要はなく、0次補間で十分である。

Sin(3*X) + Cos(3*Y) ゼロクロス法
○方法
二次元処理は以下のようにする。
f(X,Y) に於いて、
-
あるピクセルの関数値を求める。
-
もし、値が0のピクセルであれば、そのピクセル位置を0点とする。そうでなければ以下を行う。
-
ゼロクロス点を見つける。
・X軸方向の有効な隣接ピクセルを選ぶ。有効とは、無限大、非数値でないこと。
・その間で関数値の極性反転があれば、この中にZ=0 があると予測し、関数値の絶対値が小さい方のピクセルの位置をゼロクロス点とする。(0次補間あるいは最近傍補間)
・Y軸方向についても同様の処理を行う。 -
これを全てのピクセルにて行う。1.へ。
閾値法とは異なり、この方法では描画点数は激減するので、0点あるいはゼロクロス点のPoint配列を生成する。処理時間が掛かるので途中経過を表示した方が良い。
○実例
MySFはSmartFormulaのインスタンス
FCntは変数の数
Xs、Ysは変数の開始値
dX、dYは変数の刻み値
FV(,)は関数値の絶対値の配列
FS(,)は関数値の符号配列
PO()はPoint配列
'ゼロクロス点予測処理
Bmp = New Bitmap(WH, WH,
Drawing.Imaging.PixelFormat.Format32bppArgb)
Dim g As Graphics = Graphics.FromImage(Bmp)
g.Clear(Color.White)
'グラフ領域を白でクリア
g.Dispose()
gc = 0
For i = 0 To FCnt - 1
For j = 0 To FCnt - 1
Gv=0
F = MySF.FunctionValue(Xs
+ i * dX, Ys + j * dY)
FV(i, j) = Abs(F)
If Double.IsInfinity(F) OrElse Double.IsNaN(F)
Then
FS(i, j) = 0
'極性反転には参加しない点
Else
FS(i, j) = Sign(F)
If F = 0 Then
'0点
ReDim
Preserve PO(gc)
mi = i
mj = j
PO(gc).X = mi
PO(gc).Y = mj
gc = gc + 1
Gv=1
Else
If i > 0 Then
'X方向符号反転検査
If Abs(FS(i, j) - FS(i - 1, j)) = 2 Then
If FV(i, j) < FV(i - 1, j) Then
mi = i
mj = j
Else
mi = i - 1
mj = j
End If
ReDim Preserve PO(gc)
PO(gc).X = mi
PO(gc).Y = mj
gc = gc + 1
Gv=1
End If
End If
If j > 0 Then
'Y方向符号反転検査
If Abs(FS(i, j) - FS(i, j - 1)) = 2 Then
If FV(i, j) < FV(i, j - 1) Then
mi = i
mj = j
Else
mi = i
mj = j - 1
End If
ReDim Preserve PO(gc)
PO(gc).X = mi
PO(gc).Y = mj
gc = gc + 1
Gv=1
End If
End If
End If
End If
If Gv = 1 Then
Bmp.SetPixel(mi * WH / FCnt, mj
* WH / FCnt, Color.Black)
End If
Next
Me.Invalidate '途中経過を表示
Application.DoEvents()
Next
WHは表示領域サイズ(正方形の辺長)
Private Sub frmImpF_Paint(ByVal sender As Object, ByVal e As
System.Windows.Forms.PaintEventArgs) Handles MyBase.Paint
Dim g As Graphics = e.Graphics
Dim Rec As New Rectangle((Me.ClientSize.Width - WH) / 2, 10, WH,
WH)
g.DrawImage(Bmp, New PointF(Rec.Left, Rec.Top))
End Sub