S0004 モンテカルロ法

[ ホーム ] [ TIPS ウィンドウズ系 ] [ TIPS グラフィックス系 ] [ TIPS メルチメディア系 ] [ TIPS 理数系 ] [ TIPS 総覧 ]

上へ
S0001 数式処理
S0002 数式演算
S0003 陰関数のグラフ
S0004 モンテカルロ法
S0005 最小自乗法
S0006 高速冪乗算
S0007 正規乱数
S0008 相関係数
S0101 高速ソート
S0102 高速検索

VB.NET2005 TIPS / 理数系

S0004 モンテカルロ法

最終更新：2006/11/12　再掲

●解説

　モンテカルロ法とは、現在では、乱数を用いたシミュレーションを何度も行なうことにより近似解を求める計算手法のことを一般に言い、代数的に解けない問題などを解くために用いられる。近年、コンピュータの性能が著しく向上したため、有意義な手法の一つとされている。

　ここでは、モンテカルロ法にて以下を行ったので紹介する。

πを求める
定積分値(∫1/(1+X²)dX：0≦X≦1)を求める
楕円の面積を求める
球の体積を求める

●原理

○求積に関するモンテカルロ法の原理

一つの限られた空間(矩形、直方体など)を定義する。
その空間内の点を一様乱数で生成する。
その点が、対象となる関数域内か判断し、内であればカウントする。
乱数を多数生成し、繰り返す。
域内のカウント値と全体の点数の比が基本的には求める値の近似値に比例する。

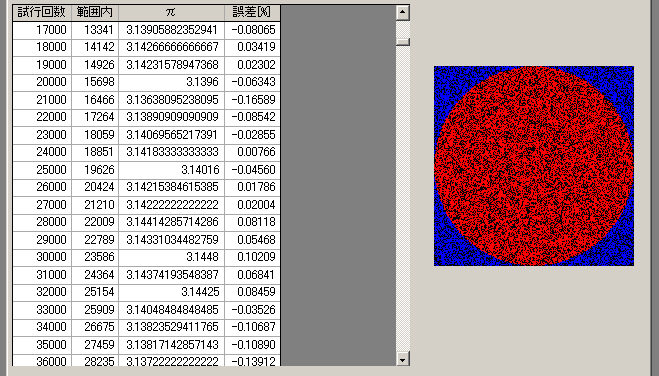
○π

　これは、半径1の円の面積を求めることと同じ。今、一辺が2の正方形を考える。この中に入る二つの一様乱数[0≦r＜2]をX_i、Y_iなる点とし、正方形の中心からの距離Rを計算する。もし、この距離が、1以内であれば、域内とカウントする。これを何度も繰り返す。域内点の個数をCとし、全ての点数をTとすれば、域内点が現われた確率は、C/Tであるが、一様乱数のため、点は正方形内に等分布していると期待できるので、結局、半径1である円(正方形に内接する円)の面積は、正方形の面積に域内点の確率を掛けたものとなる。つまり、4*C/T　となる。これが、半径1の面積(π*1*1)なので、すなわち、π そのものとなる。

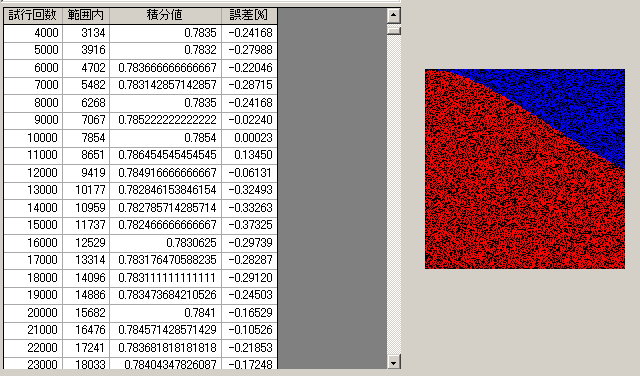
○定積分値

　今、一辺が1の正方形を考える。この中に入る二つの一様乱数[0≦r＜1]をX_i、Y_iなる点とし、Yiが、関数値(1/(1+X_i²))以内であれば、域内とカウントしする。このカウント値Cと全数Tの比(C/T)は定積分値に近づく。

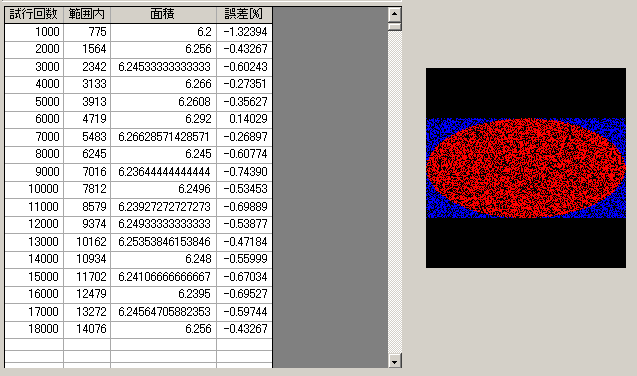
○楕円の面積

　横4、縦2の矩形を考える(長径2、短径1の楕円を想定)。この中に入る二つの一様乱数[-2≦r＜2]をX_i、[-1≦r＜1]をY_iなる点とし、関数値(X_i²/2²+Y_i²/1²)が1以内であれば、域内とカウントしする。このカウント値Cと全数Tで算出される(8*C/T)は楕円の面積(π*2*1)に近づく。

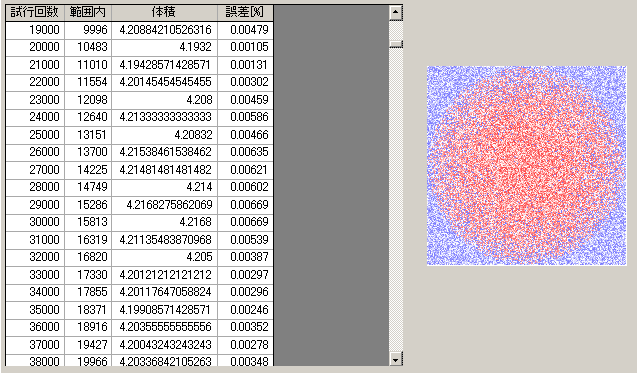
○球の体積

　一辺が2の正立方体を考える(半径1の球体を想定)。この中に入る三つの一様乱数[0≦r＜2]を空間の点とし、正立方体の中心からの距離を求め、それが1以内であれば、域内としてカウントする。このカウント値Cと全数Tで算出される(8*C/T)は球体積(4/3*π)に近づく。

●方法

アルゴリスムは上記。
途中経過をビジュアルに見せる工夫を行う。乱数で発生する点数は数十万点以上になるので、通常にグラフィック表示すると負荷が重すぎ具合が悪い。この場合は、ビットマップを利用する。発生した点をビットマップのピクセルに対応させ、SetPixel関数で反映する。ある程度点数が溜まったら、ピクチャボックスのImageプロパティに割り付ける。Imageプロパティは再描画なしで表示されるので都合がよい。ビットマップは200X200とする。
また、途中経過の数値を表にして見せるなどすれば更に良い。

●事例

bmpは、ビットマップ
frgRは、結果を数値表示する私製グリッドコントロール
picPは結果を表示するピクチャボックス
域内点は赤、その他は青で表示される
lstMはリストボックスで、メニューがリストされている

1000点ごとに途中経過を表示し、これを300回繰り返す。

Dim X, Y, Z, XL, YL, ZL As Single
Dim R, P As Double
Cnt = 0 : InC = 0 : LC = 0
Me.Cursor = Cursors.WaitCursor
Application.DoEvents()
Select Case lstM.SelectedIndex
   Case 0           'π
      bmp = New Bitmap(200, 200, Drawing.Imaging.PixelFormat.Format32bppRgb)
      frgR.SetGridConstruction(4, 301, 0, 1)
      frgR.RowHeader(0) = Hdra
      frgR.ColTextFormat(3) = "0.00000"
      Do
         X = Rnd() * 2.0F
         Y = Rnd() * 2.0F
         XL = X - 1.0F
         YL = Y - 1.0F
         R = Sqrt(XL * XL + YL * YL)   '中心からの距離
         Cnt = Cnt + 1            '乱数のセット数
         XL = X * 99.5
         If XL >= 199 Then XL = 199
         YL = Y * 99.5
         If YL >= 199 Then YL = 199
         If R <= 1.0 Then
            InC = InC + 1      '域内
            bmp.SetPixel(XL, YL, Color.Red)
         Else
            bmp.SetPixel(XL, YL, Color.Blue)
         End If
         If LC > 300 Then Exit Do
         If Cnt > 0 AndAlso (Cnt Mod 1000) = 0 Then    '1000毎に表示
            frgR.BeginUpdate()
            frgR(0, LC + 1) = Cnt
            frgR(1, LC + 1) = InC
            P = 4.0 * InC / Cnt             'πの近似値
            frgR(2, LC + 1) = P
            frgR(3, LC + 1) = (P - PI) / PI * 100
            frgR.EndUpdate()
            frgR.TopRow = LC
            Application.DoEvents()
            LC = LC + 1
            picP.Image = bmp
         End If
         If Abort = 1 Then Exit Do
      Loop
   Case 1             '定積分値
      bmp = New Bitmap(200, 200, Drawing.Imaging.PixelFormat.Format32bppRgb)
      frgR.SetGridConstruction(4, 301, 0, 1)
      frgR.RowHeader(0) = Hdrb
      frgR.ColTextFormat(3) = "0.00000"
      Do
         X = Rnd()
         Y = Rnd()
         R = 1.0 / (1.0 + X * X)
         Cnt = Cnt + 1
         XL = X * 199
         If XL >= 199 Then XL = 199
         YL = Y * 199
         If YL >= 199 Then YL = 199
         If Y <= R Then
            InC = InC + 1
            bmp.SetPixel(XL, 199 - YL, Color.Red)
         Else
            bmp.SetPixel(XL, 199 - YL, Color.Blue)
         End If
         If LC > 300 Then Exit Do
         If Cnt > 0 AndAlso (Cnt Mod 1000) = 0 Then
            frgR.BeginUpdate()
            frgR(0, LC + 1) = Cnt
            frgR(1, LC + 1) = InC
            P = InC / Cnt
            frgR(2, LC + 1) = P
            frgR(3, LC + 1) = (P - PI / 4.0) / (PI / 4.0) * 100
            frgR.EndUpdate()
            frgR.TopRow = LC
            Application.DoEvents()
            LC = LC + 1
            picP.Image = bmp
         End If
         If Abort = 1 Then Exit Do
      Loop
   Case 2             '楕円の面積
      Dim A, B, AA, BB As Single
      bmp = New Bitmap(200, 200, Drawing.Imaging.PixelFormat.Format32bppRgb)
      frgR.SetGridConstruction(4, 301, 0, 1)
      frgR.RowHeader(0) = Hdrc
      frgR.ColTextFormat(3) = "0.00000"
      A = 2.0
      B = 1.0
      AA = A * A
      BB = B * B
      Do
         X = Rnd() * 2 * A - A
         Y = Rnd() * 2 * B - B
         R = X * X / AA + Y * Y / BB
         Cnt = Cnt + 1
         XL = (X + A) / (2.0 * A) * 199
         If XL >= 199 Then XL = 199
         YL = (Y + B) / (2.0 * B) * (199 * B / A)
         If YL >= 199 Then YL = 199
         If R <= 1.0 Then
            InC = InC + 1
            bmp.SetPixel(XL, YL + 50, Color.Red)
         Else
            bmp.SetPixel(XL, YL + 50, Color.Blue)
         End If
         If LC > 300 Then Exit Do
         If Cnt > 0 AndAlso (Cnt Mod 1000) = 0 Then
            frgR.BeginUpdate()
            frgR(0, LC + 1) = Cnt
            frgR(1, LC + 1) = InC
            P = 4.0 * A * B * InC / Cnt
            frgR(2, LC + 1) = P
            frgR(3, LC + 1) = (P - A * B * PI) / (A * B * PI) * 100
            frgR.EndUpdate()
            frgR.TopRow = LC
            Application.DoEvents()
            LC = LC + 1
            picP.Image = bmp
         End If
         If Abort = 1 Then Exit Do
      Loop
   Case 3         '球の体積
      bmp = New Bitmap(200, 200, Drawing.Imaging.PixelFormat.Format32bppArgb)
      frgR.SetGridConstruction(4, 301, 0, 1)
      frgR.RowHeader(0) = Hdrd
      frgR.ColTextFormat(3) = "0.00000"
      Do
         X = Rnd() * 2.0
         Y = Rnd() * 2.0
         Z = Rnd() * 2.0
         XL = X - 1.0
         YL = Y - 1.0
         ZL = Z - 1.0
         R = Sqrt(XL * XL + YL * YL + ZL * ZL)
         Cnt = Cnt + 1
         If R <= 1.0 Then
            InC = InC + 1
            bmp.SetPixel(X * 99, Y * 99, Color.FromArgb(Z * 100, 255, 0, 0))
         Else
            bmp.SetPixel(X * 99, Y * 99, Color.FromArgb(Z * 70, 0, 0, 255))
         End If
         If LC > 300 Then Exit Do
         If Cnt > 0 AndAlso (Cnt Mod 1000) = 0 Then
         frgR.BeginUpdate()
         frgR(0, LC + 1) = Cnt
         frgR(1, LC + 1) = InC
         P = 8.0 * InC / Cnt
         frgR(2, LC + 1) = P
         frgR(3, LC + 1) = (P - 4 / 3 * PI) / (4 / 3 * PI)
         frgR.EndUpdate()
         frgR.TopRow = LC
         Application.DoEvents()
         LC = LC + 1
         picP.Image = bmp
      End If
      If Abort = 1 Then Exit Do
   Loop
End Select
Me.Cursor = Cursors.Default
Abort = 0

●実行例

　上記コードで実行した途中経過。