|
‹ZЏp‰рђа |
|
‰AЉЦђ”‚МЌ‚‘¬•`‰ж‡U |
| ЌЕЏIЌXђV“ъЃF2007/05/15Ѓ@ ђV‹K |
ЃњЉT—vЃ@
Ѓ@ЉЦђ”‚𕶎љЋ®‚Е—^‚¦‚ЅЏкЌ‡ЃAЉЦђ”‚М‰‰ЋZ‚ЙЋћЉФ‚ЄЉ|‚©‚й(ѓRЃ[ѓh‚МѓRЃ[ѓ‹ѓoѓbѓN‚Мђ”Џ\”{€ИЏг)‚М‚ЕЃA‚Ь‚Ж‚а‚Й•`‰ж‚·‚й‚ЖЃAЋћЉФ‚ЄЉ|‚©‚и‚·‚¬‚йЃB
Ѓ@‰AЉЦђ”‚МЏкЌ‡ЃAЉЦђ”’l‚р‹Ѓ‚Я‚й‰сђ”‚НЃA—zЉЦђ”‚МЏкЌ‡‚М–}‚»Ћ©Џж”{‚Й‚И‚йЃB‚В‚Ь‚иЃA—zЉЦђ”‚Е1000“_‚Ж‚·‚к‚ОЃA‰AЉЦђ”‚Е‚НЃA1000 X 1000 = 100–њ‚Ж‚И‚Б‚Д‚µ‚Ь‚¤ЃB—zЉЦђ”‚М1000”{‚М‰‰ЋZђ”‚Й‰Б‚¦ЃA•¶ЋљЋ®‰‰ЋZ‚И‚М‚ЕЃAѓRЃ[ѓh‚Й‚ж‚йЉЦђ”‚МѓRЃ[ѓ‹ѓoѓbѓN‚ж‚иђ”Џ\”{‚МЋћЉФ‚Є‚©‚©‚йЃB
ЃњЊґ—ќ
Ѓ@‰єђ}ЋQЏЖЃB
Ѓ›‘e•`‰ж
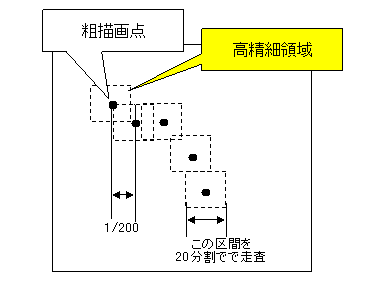
Ѓ@‘S‘М‘њ‚р‘Ѓ‚’Н‚Ю€У–Ў‚ЕЃAђж‚ёЃA‘e‚ў•`‰ж‚рЋЋ‚Э‚йЃBЏc‰Ў‚Е 200 X 200 ‚Ж‚µ‚ДЉЦђ”’l‚р‹Ѓ‚ЯЃA•„Ќ†”Ѕ“]‚рЊџЏo‚·‚йЃB‚±‚МЏу‘Ф‚Е‚Н‚»‚к‚И‚и‚М‘¬“x‚Ж‚И‚й‚М‚ЕЃAѓCѓ“ѓ^ѓ‰ѓNѓeѓBѓuЏ€—ќ‚Є‰В”\‚Ж‚И‚йЃB ‘S‘М‚Ж‚µ‚Д‚МЊXЊь‚р•\‚№‚й‚ЄЃA•Є‰р”\€И‰є‚М•П‰»‚НЊџЏo‚Е‚«‚И‚ўЃB
Ѓ›Ќ‚ђёЌЧ
Ѓ@‘e•`‰ж‚Е‚НЃA‹Иђь‚Ж‚µ‚Д‚Н–ўЉ®ђ¬‚И‚М‚ЕЃAЌ‚ђёЌЧ‚Е•`‰ж‚·‚йЃBЌ‚ђёЌЧ‚Е‚НЃAЌЏ‚Э‚НЃA1200 X 1200 ‚ЕЃA’КЏн‚Ж“Ї‚¶ђё“x‚Ж‚И‚йЃB‚µ‚©‚µЃA‚Ь‚Ж‚а‚Й‰‰ЋZ‚·‚й‚ЖЋћЉФ‚ЄЉ|‚©‚й‚М‚ЕЃA‘e•`‰ж‚Е‹Ѓ‚Я‚з‚к‚Ѕ•„Ќ†”Ѕ“]ЌА•W‚р’†ђS‚Й‚µЃA1200ЌЏ‚Э‚Е -10Ѓ`+10 ‚М‹йЊ`—М€ж‚рЌ‚ђёЌЧ‚Е•„Ќ†”Ѕ“]€К’u‚рЊџЏo‚·‚йЃB‚±‚М•ы–@‚Е‚НЃA‘S€ж‚р‘–Ќё‚·‚й‚ж‚艉ЋZђ”‚Єђ”•Є‚М1‚©‚зђ”Џ\•Є‚М1‚Й‚И‚й‚ЖЉъ‘Т‚Е‚«‚йЃB’A‚µЃA‘e•`‰ж‚Й‚И‚ўЌА•W“_‚Н‘–Ќё‚і‚к‚И‚ў‚М‚ЕЃA•”•Є“I‚Й”І‚Ї‚Єђ¶‚¶‚йЏкЌ‡‚а‚ ‚йЃB‚±‚М•ы–@‚Е‚аЋћЉФ‚НЉ|‚©‚й‚М‚Е‰‰ЋZ“r’†Њo‰Я‚р•\Ћ¦‚·‚йЃB
Ѓ@
Ѓ@