|
技術解説(数学関数編) |
|
正弦/余弦(sin/cos) |
| 最終更新日:2007/04/26 再掲 |
●概要
級数展開にて求める。但し、そのままでは収束が遅いので工夫が必要となる。
●級数
○定義
以下の展開式を用いる。
・sin(x) = ∑(-1)k * x(2*k+1) /(2 * k + 1)! [k = 0 to ∞]
・cos(x) = ∑(-1)k * x(2*k) /(2 * k)! [k = 0 to ∞]
○収束の予測
sin、cos の収束はほぼ同じで、SeriesLastItem関数にて展開した下表のようになる。
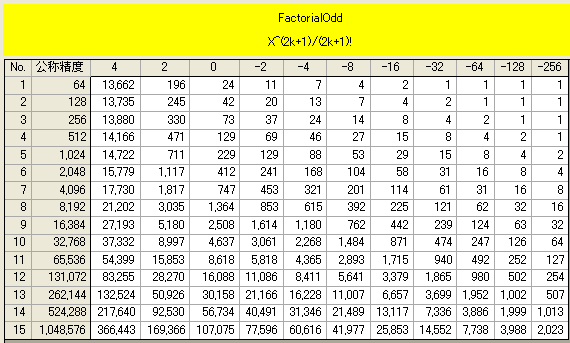
そのまま、級数で演算すれば、上表で、変数オーダが 0 の部分に相当する。100万桁では、約10万項となり、時間は掛かりそう。
●高速化
与えられた任意のXを小さくする。指数関数のような法則はないので、倍角公式を応用する。
○倍角公式
具体的に説明する。cos の2倍角公式は、
cos(2 * X) = 2 * (cos(X))2 - 1
であるが、これではピンとこないので、変数を置き換えると、
cos(X) = 2 * (cos(X / 2))2 - 1
となる。この式を良く見ると、cos(X) を求めるには、半分のX/2 をまづ求めれば、算出できると言っている。つまり、変数を半分にできた。更に、
cos(X / 2) = 2 * (cos(X / 4))2 - 1
とできる。列挙すれば、
cos(X) = 2 * (cos(X / 2))2 - 1
cos(X / 2) = 2 * (cos(X / 4))2 - 1
cos(X / 4) = 2 * (cos(X / 8))2 - 1
cos(X / 8) = 2 * (cos(X / 16))2 - 1
精度や演算数を無視すれば、X は際限なく小さくできる。これらは、漸化式となるので、X/2n について級数で求め、後は漸化式で X/20 まで遡れば良い。
○N倍角公式
2倍では効率が悪いので、大きな数のsin/cos の倍角公式を見ると、
・3倍角の公式
sin3θ=3sinθ-4sin3θ
cos3θ=4cos3θ-3cosθ
・4倍角の公式
sin4θ=4sinθcosθ-8sin3θcosθ
cos4θ=8cos4θ-8cos2θ+1
・5倍角の公式
sin5θ=16sin5θ-20sin3θ+5sinθ
cos5θ=16cos5θ-20cos3θ+5cosθ
となる。
○適用する倍角
対となる関数が現れる倍角公式は使えない。3倍角では、1/3 が、徒に語長をのばしてしまう可能性が高い。sin、cos で、同じ漸化式になり、効率が高い5倍角が良さそうである。
○段数
5倍角では、段数を n とすれば、変数は、X/5n にできる。変数は、高々6 (2π)程度なので、
- 10段:1/9,765,625 = 0.0000001024 (10-7)
- 20段:1/95,367,431,640,625 = 0.00000000000001048576 (10-14)
10 ~20 段が候補。これにて、100万桁では、3~4万項となり、何もしないときよりは数倍の速度で収束する。
○漸化式の演算方式
Y = 16 * X5 - 20 * X3 + 5 * X
の演算方式による回数を見積もると、下表のようになる。
| 方式 | Mul | MulI | Add |
| 16 * X5 - 20 * X3 + 5 * X | 4 | 3 | 2 |
| X * (16 * X4 - 20 * X2 + 5) | 3 | 2 | 2 |
| X * (X2 * (16 * X2 - 20) + 5) | 3 | 1 | 2 |
最後の方式が最も演算数が少なくなる。但し、16 * X2 - 20 などの演算は、精度が十分ないと桁落ちが生じるので注意が必要となる。しかし、収束判定はないので、精度が全体として落ちるだけである。一番演算数の多いものは、精度的には安全な演算となる。
●実測値
下表は、Sin(e) (e は、精度桁のネイピア数) を実際に求めた時間を計測したものである。SinBasic は、そのまま級数で演算した場合、 Sin 5^N は、漸化式を N 段にした場合である。N = 10、12、14、16、18 と変化させた。Basic はやはり遅い。4096桁以上では、20段が速くなっている。