|
技術解説(数学関数編) |
|
逆正弦/逆余弦(asin/acos) |
| 最終更新日:2007/04/26 再掲 |
●概要
級数展開にて求める。但し、そのままでは収束が遅いので工夫が必要となる。
●級数
○定義
以下の展開式を用いる。
・asin(X) = ∑ (2 * k - 1)!!/((2 * k)!! * (2 * k + 1)) * X(2*k+1) [k = 0 to ∞]
・逆余弦は、acos(X) = π/2 - asin(X) から求める。
○収束の予測
係数は、分母分子に二重階乗があり、これにより、相殺され、係数部分の収束は全く期待できない。

変数のオーダは -1 以上なので、100万桁では、50万項以上必要になるので、収束は期待できない。
●高速化
結局、X を小さくするしかない。
○余角
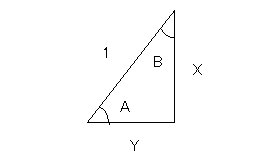
上図において、
A = π / 2 - B
であるから、
asin(X) = π / 2 - asin(Y)
ところで、
X2 + Y2 = 1
だから、
asin(Y) = asin(sqrt(1 - X2))
となる。sqrt(1 - X2) は、X が、1 に近いほど、小さくなるので、収束が期待できる。 余角を採用する判定は、
X > sqrt(1 - X2)
を解けばよい。これを解くと、
X > 1 / sqrt(2) = 0.7
つまり、|X| が 0.7以上の場合は、余角を採用する。
○加法定理 (差分法)
自然対数と同じコンセプトの方法である。sin の加法定理は、
sin(α - β) = sin(α)*cos(β) - sin(β)*cos(α)
であるが、これを arc で表現すると、、
α - β = asin(sin(α)*cos(β) - sin(β)*cos(α))
となる。今、sin(α) = x、sin(β) = y とすれば、
α = asin(x)、β = asin(y)
cos(β) = sqrt(1 - y2)、cos(α) = sqrt(1 - x2)
なので、
asin(x) - asin(y) = asin(x*sqrt(1 - y2) - y*sqrt(1 - x2))
と、よく知られた関係式となる。ここで、
z = x*sqrt(1 - y2) - y*sqrt(1 - x2)
とおいて、変形すると、
asin(x) = asin(y) + asin(z)
与えられた値をx とすれば、asin(y) + asin(z) を求めれば良い。y と z は、上記の関係内であれば任意なので、今、
asin(y) =[asin(x)]
→ [n] は、限りなく真値 n に近いと言う意味。
ここでの真値とは、求める精度での値。
とすれば、asin(z) は、限りなく0に近く(つまり、ラフ値と真値との差分)にならざるを得なくなる。つまり、z もそうなる。
[asin(x)] は、組込み関数で、求めれば、15桁の精度の値が得られる。この値を使い、多倍長(目標精度)で、
y = sin([asin(x)])
を求め、z を算出し、この z にて級数を求め [asin(x)] + asin(z) とする。
●適用
余角と差分法の両方を適用するか、差分法のみかであるが、差分法は変数に範囲に限らず成立するので、差分法のみの適用で十分であろう。余計な演算(平方根や自乗演算)が減る分得かも知れない。
●実測値
下図は、上記の高速化を適用した演算時間の実測値である。
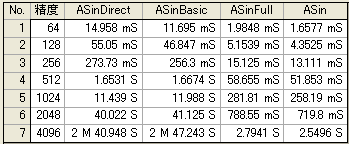
ASin(0.777777) を演算した時間で、
-
ASinDirect :級数そのまま
-
ASinBasic :余角を適用
-
ASinFull :余角と差分法を適用
-
ASin :差分法のみ適用
となっている。差分法の効果は絶大である。また、差分法のみの適用が良いことが分かる。