双曲線正弦/余弦

技術解説(数学関数編)

双曲線正弦/余弦(sinh/cosh)

最終更新日：2007/04/26　新規

●概要

　定義式で求めるか、級数で求めるか迷う所である。

●定義

・sinh X = (e^X - e^-X) / 2

・cosh X = (e^X + e^-X) / 2

●級数

　・sinh X = Σ X^(2*k+1) /(2 * k + 1)! [k = 0 to ∞]

　・cosh X = Σ X^(2*k) /(2 * k)! [k = 0 to ∞]

　であるが、これは、sin、cos と同型で、収束傾向も同じ。但し、変数の範囲が頗る広いので、大きいところでは無理。

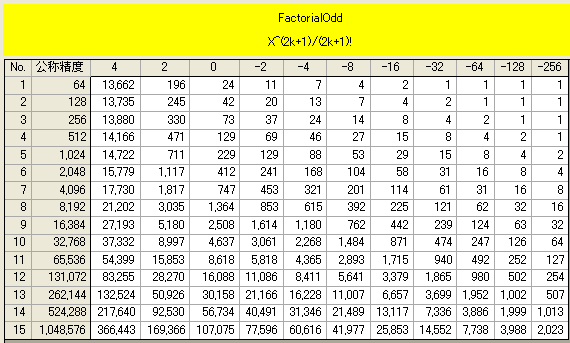
(再掲) sinh/cosh の収束(その精度を得るための k の値)

●5角公式

　双曲線でも、三角関数と同じように倍角公式があり、5倍角は以下の通りである。

・sinh5X = 16sinh⁵X + 20sinh³X + 5sinhX

・cosh5X = 16cosh⁵X - 20cosh³X + 5coshX

　これを漸化式にすれば、m 段で、1/5^m にできる。

●見積り

○定義式

　定義式での演算では、 e^X の算出とその逆数演算が主要演算で残りは無視できる。e^X の演算は、X の小数部での級数演算なので、収束はほぼ一定しており、また1/Nや分割方式で演算されるので、変数の広い範囲で安定な収束となっている。16384桁で20秒以下。

○級数＋倍角

　これは、sin と同じと考えてよく、漸化式15段程度で、16384桁が20秒以下。

級数＋倍角で求めるまでもなく、変数の全ての範囲で定義式で求めても良さそう。

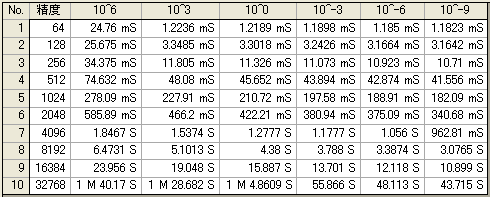
●実測値

○定義式

　下表は、定義式にて演算した時間である。横軸は変数のオーダで、10⁶ ～ 10^-9 まで測定した。

変数の広い範囲で安定した演算時間となっている。

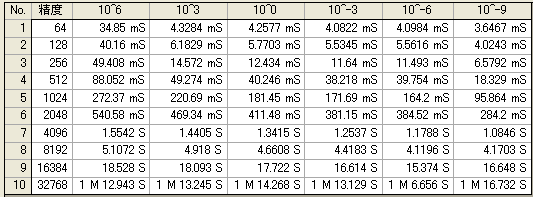
○級数＋漸化式15段

○級数＋漸化式20段