[ ホーム ] [ 概要 ] [ プログラミング仕様 ] [ 演算速度 ] [ 技術解説(システム編) ] [ 技術解説(四則演算編) ] [ 技術解説(FFT編) ] [ 技術解説(数学関数編) ]

上へ
高速化手法
平方根/立方根
整数指数
指数関数
実数指数
自然対数
一般対数
正弦/余弦
正接
逆正弦/逆余弦
逆正接
双曲線正弦/余弦
双曲線正接
逆双曲線関数

●概要

　指数関数では、指数が整数ではなく、実数となるので、単純な冪乗では求められない。級数展開を利用する。

●原理

　級数を利用する場合は、指数X をそのままでは、級数の収束が保証できなくなるので、工夫が要る。

○級数

　e^X = ��(X^k / k!)            (k = 0 to ∞)

○整数、小数分離

 e^X において、

  X = I + F     (I = 整数部、 F = 小数部 ＜ 1)

とすれば、

e^X = e^(I+F) = e^I ・e^F

となる。 e^I は、整数指数の2進展開法で高速に求められる。但し、目標精度のネイピア数 e を定数として準備しておく必要がある。結局、e^F を求めることに帰着される。

●高速化

　F は、1 よりは小さいことが分っているが、最悪は、0.99999 ≒ 1 なので、級数の項数が増加しても、オーダは不変で、分母で収束が決まってしまう。従って、F を更に小さくする。

○１/N

  F = U・N (N は正整数)とすれば、U = F/N であるが、

e^F = e^U・N = e^(F/N)・N
    = (e^(F/N))^N

となるので、U(F/N) 乗の演算になる。N 乗は、整数指数の2進展開法で高速に求められる。

○分割

　e^U = e^U0・e^U1・e^U2・・・・・　　　但し、U = ΣUi

とできる。分割は任意なので、Ui = mi・10^-a・i(mi ＜ 1) とできる。例えば、a = 8 (つまり基数の単位指数) とすれば、仮数部配列の要素単位となり、U は、-8、-16、-24 などのオーダになり、それぞれの級数の収束は格段に早まる。以上ことを図示すれば下図のようになる。Fの指数が 0 の場合のイメージである。

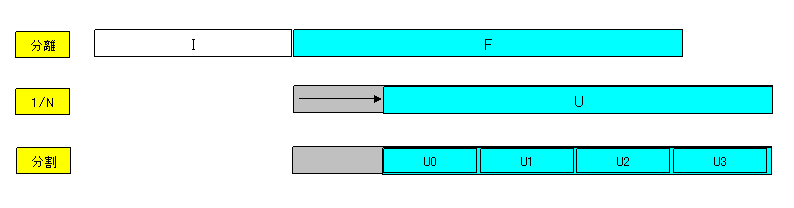
　分割のもう一つの効果は、U の桁数が 8 桁以内になることで、級数の X^(k+1) = X^k・X なる乗算が、多倍長とBase の乗算で済むことになり、極めて速くなる可能性がある。また、k も比較的小さくなるので、1/(k+1)! = 1/k!/(k+1) なる分母の演算も、多倍長とBase の除算で済む可能性が高くなる。

●演算内容例

　以下のような演算を行っている。

1. 指数 X が、負であれば、正にし、逆数フラグをたてておく。
2. X を、整数 I と小数 F に分離する。
3. F の指数が、-8 より大きければ、U = F / 10⁸ とする。
4. U を 8 桁づつ、最大で4 分割する(U の桁数によって変化する)。但し最後は残り桁全てとなる。
5. 分割された各Ui で、級数で値を求め、その全てを乗積する。
6. 1/10⁸ していたなら、結果を 100000000乗する。
7. 整数指数 I で算出した値 e^I と乗算する。
8. 逆数フラグがオンなら、値の逆数を求める。

●シミュレーション

　実測は時間がかかるので、予測ツールで上記の手法の種々の組合せの効果を予測した。

●実測値

　上記のことを実際に行った結果である。高速化を順次適用してその効果を見たものである。指数は、π にしている。つまり、e^π の演算をしている。

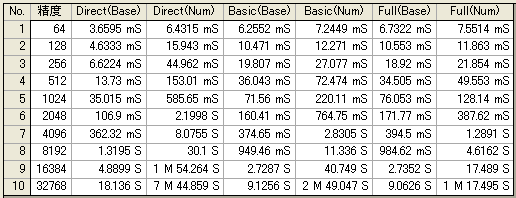
(Base) ：指数が8桁
(Num) ：指数が精度桁

Direct：指数をそのまま級数に適用
Basic ：1/10⁸ を適用
Full    ：分割も適用

Full(Base) は、演算方式は、Basic(Base) と同じ。

　同じ方式では、いずれもBaseが速くなっている。これは、多倍長*Base の演算が速くなるからである。

　桁数が大きくなると、Num では、Full が一番速い。つまり、分割は効果がある。但し、乗算回数が大変多くなり、精度低下が起こるので、精度に余裕を持たせるなどの工夫がいる。