|
技術解説(数学関数編) |
|
逆正接(atan) |
| 最終更新日:2007/04/26 再掲 |
●概要
級数展開にて求める。但し、そのままではかなり収束が遅いので工夫が必要となる。
●級数
・atan(X) = ∑(-1)k-1 * X(2*k-1) / (2 * k - 1) [k = 1 to ∞]
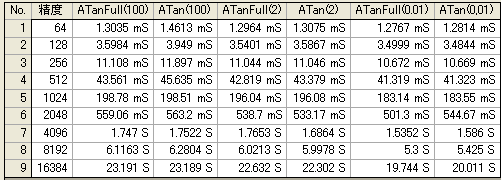
級数の収束予測を行うと、下表のように、100 以上では、とても実用できない。分母が、1次なので、なかなか小さくなってくれない。

●高速化
級数の高速化は、結局変数の微小化を行うことである。atan は、変数の範囲が広く工夫が要る。
○余角
まづ考えられるのは、余角を利用することである。
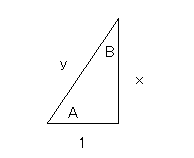
上図から、B = atan(1/x) なので、A = π/2 - B から、atan(x) = π /2 - atan(1 / x) なので、逆数から求められる。従って、X > 1 の場合は、この方式を採用する。
○既知の値との差
加法定理では、
tan(α - β) = (tan(α) - tan(β)) / (1 + tan(α) * tan(β))
となるが、これと下図より、
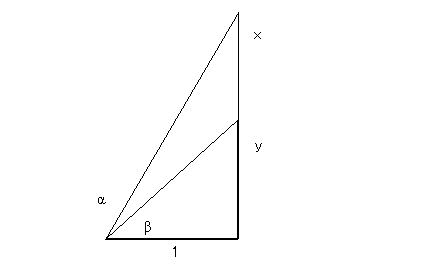
tan(α - β) = (x - y) / (1 + x * y)
だから、arc にすれば、
α - β = atan((x - y) / (1 + x * y))
今、β = π / 4 (45度) とすれば、y = 1 なので、
α - π / 4 = atan((x - 1) / (x + 1))
∴ α = π / 4 + atan((x - 1) / (x + 1))
z = (x - 1) / (x + 1)
とすれば、z < 1 となる。atan(x) は、atan(z) を求めることに帰着された。但し、闇雲に適用するのではなく、x の適当な範囲で採用する。角度にして、π/8 ~ 3π/8 が分かりよい。x にすれば、0.4 ~ 2.4 程度となる。z に換算すれば、-0.43 ~ 0.41 となる。これにて、余角については、 X > 2.4 で採用することになる。
○加法定理法 (差分法)
これまでの対策で、少なくとも変数は、0.4 以下に変換できた。しかし、0.4 程度では、100万桁では、10万項以上の計算が必要でまだまだ時間がかかる。
自然対数と同じコンセプトの方法である。加法定理から、
tan(α - β) = (x - y) / (1 + x * y) (再掲)
をarc を使って変形すると、
atan(x) - atan(y) = atan(z)
但し、z = (x - y) / (1 + x * y)
従って、
atan(x) = atan(y) + atan(z)
今、atan(y) = [atan(x)]
[n] は、限りなく真値 n に近いと言う意味。 ここでの真値とは、求める精度での値。
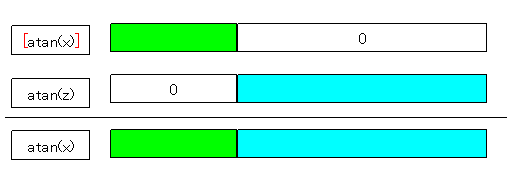
とすれば、atan(z) は、限りなく0に近く(つまり、ラフ値と真値との差分)にならざるを得なくなる。つまり、z もそうなる。下図参照。
[atan(x)] は、組込み関数で求めれば、15桁の精度の値が得られる。この値を使い、多倍長(目標精度)で、
y = tan([atan(x)])
を算出すれば、高精度な z が求まる。結局、atan(z) を求めることに帰着された。z は、非常に微小な値となり、これによる級数の収束は期待できる。
●適用
余角、π/4 との差、差分法があるが、余角、π/4 との差を施してから差分法を適用するか、差分法のみ適用するかが問題となる。差分法のミソは、z = (x - y) / (1 + x * y) の x - y であり、これが限りなく 0 に近くなれば良い。この z が、あらゆる変数の範囲で成立すれば、差分法のみで構わないことになる。x - y = ε とすれば、これは、おおむねDouble 精度である 10-15 以下の値になる。分母は、x ≒ y なので、1 + x2 として構わない。x ≪ 1 の場合は、分母は 1、x ≫ 1 の場合は、x2 となる。いずれにしても、x のあらゆる範囲で、ε < 10-15 が成立する。むしろ、x が大きい方がε は小さくなる方向。従って、差分法のみの適用で十分と言える。
●実測値
実際に上記の高速化を実施した結果である。
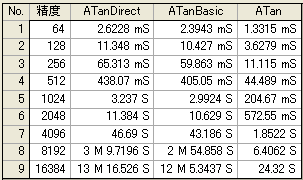
ATan(2.333333) の演算時間。
-
ATanDirect :1/2.333333 なる余角のみ
-
ATanBasic :既知との差
-
ATan :差分法のみ
下図は、ATanFull (余角や既知との差の後、差分法を適用)と差分法のみの比較である。そんなに差はないことが分かる。()内は変数の値。