[ ホーム ] [ 高速化手法 ] [ 平方根/立方根 ] [ 整数指数 ] [ 指数関数 ] [ 実数指数 ] [ 自然対数 ] [ 一般対数 ] [ 正弦/余弦 ] [ 正接 ] [ 逆正弦/逆余弦 ] [ 逆正接 ] [ 双曲線正弦/余弦 ] [ 双曲線正接 ] [ 逆双曲線関数 ]

上へ

●概要

　実測は時間がかかるので、予測ツールで高速化手法の種々の組合せの効果を予測した。

●シミュレーション条件

　変数は公称精度桁の多倍長で、オーダは 0 とする。環境は筆者のP4 3.2GHz マシン。

●1/N

　級数原型は、級数でそのまま演算した場合で、基準値となる。

　N は、10⁶ 〜 10¹⁸ まで予測した。1/N した変数での級数展開時間と、その結果を N乗 する時間の合計である。

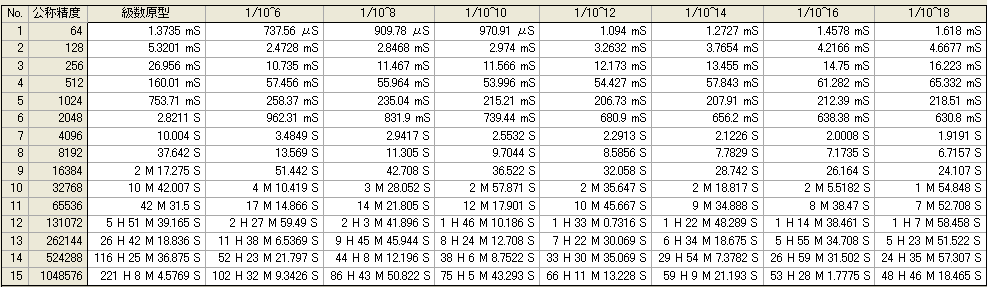
　とりあえず、2000桁以上では、N が大きいほど効果があると分かった。

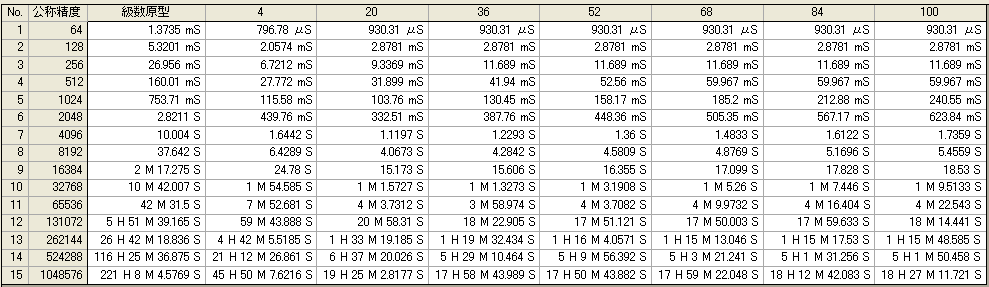
●分割

　変数を 8桁単位で分割した場合。1/Nはしない。分割数を 4 〜 100 まで変化させている。